【第14讲】二重积分整理
-
椭圆面积公式: $$ S_{椭圆}=\pi ab $$
-
\((x,y)\) 关于 \(x=a\) 的对称点: $$ (2a-x, y) $$
-
一个用到多次的公式: $$ \left( \frac{\sin \theta}{\cos \theta+\sin \theta} \right)'=\frac{1}{(\cos \theta+\sin \theta)^{2}}. $$
个人认为这类公式也要“背”,但这里背诵的意义更多是为了在真正实战时看到类似的形式可以成为人形“哈希”,能直接以 \(O(1)\) 的时间复杂度映射出来,不容许在这种能把握的地方失分。 这种步骤一般只会是一个关键步骤,但可能起到做出一整道题目的决定性作用。
-
性质:
- 线性性质:\(\iint_{D}[k_{1}f(x,y)\pm k_{2}g(x,y)]d_{\sigma}=k_{1}\iint_{D}f(x,y)d_{\sigma}\pm k_{2}\iint_{D}g(x,y)d_{\sigma}\)
- 可加性:\(\iint_{D}f(x,y)d_{\sigma}=\iint_{D_{1}}f(x,y)d_{\sigma}+\iint_{D_{2}}f(x,y)d_{\sigma}\)
- 保号性:\(f(x,y)\leq g(x,y)\),则有 \(\iint_{D}f(x,y) d_{\sigma}\leq \iint_{D}g(x,y) d_{\sigma}\)
- 求面积区域:\(\iint_{D}d_{\sigma}=A\)
- 必要性:可积函数必有界
- 估值定理:\(mL\leq\iint_{D}f(x,y)\leq ML\)
- 中值定理:\(\iint_{D}f(x,y)d_{\sigma}=f(\xi_{i},\eta_{i})A\)
-
轮换对称性
$$ \iint_{D}f(x,y)d_{x}d_{y}=\iint_{D}f(y,x)d_{y}d_{x}. $$ 6. 二重积分在直角坐标系下的计算口诀: - 后积先定限, - 限内画条线, - 先交定下限, - 后交定上限。
- 二重积分在极坐标系下的小区域 $$ d_{\sigma}=d_{r}\cdot rd_{\theta} $$
-
二重积分在极坐标系下的表达式 $$ \iint_{D}f(x,y)d_{\sigma}=\int_{\alpha}{\beta}d_{\theta}\int_{r_{1}(\theta)} $$}(\theta)}f(r\cos \theta, r \sin \theta) r d_{r
-
一个特殊的积分: $$ \int_{-\infty}^{+\infty} e{-x. $$}}dx = \sqrt{ \pi
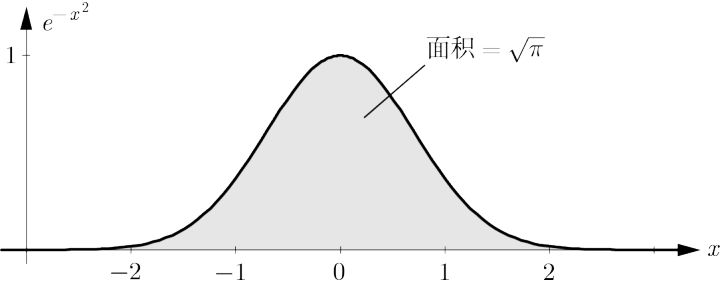
-
二重积分换元法表达式: $$ \iint_{D_{xy}}f(x,y)d_{x}d_{y} \xlongequal{x=x(u,v),y=y(u,v)}\iint_{D_{uv}}f[x(u,v),y(u,v)]\left|\frac{\vartheta(x,y)}{\vartheta(u,v)}\right|d_{u}d_{v} $$
-
雅可比行列式: $$ \frac{\vartheta(x,y)}{\vartheta(u,v)} = \begin{vmatrix} \frac{\vartheta x}{\vartheta u} & \frac{\vartheta x}{\vartheta v} \ \frac{\vartheta y}{\vartheta u} & \frac{\vartheta y}{\vartheta v} \ \end{vmatrix}\quad\neq 0 $$