【第16讲】无穷级数
- \(p\) 级数(实际上是第 268 页的内容,但当时未整理,现遗忘)
\[
\int_{0}^{1} \frac{1}{x^{p}}dx
\begin{cases}
\text{收敛}, 0<p<1, \\
\text{发散}, p\geq 1.
\end{cases}
$$
$$
\int_{0}^{+\infty} \frac{1}{x^{p}} dx
\begin{cases}
\text{收敛}, p>1, \\
\text{发散}, p\leq 1.
\end{cases}
\]
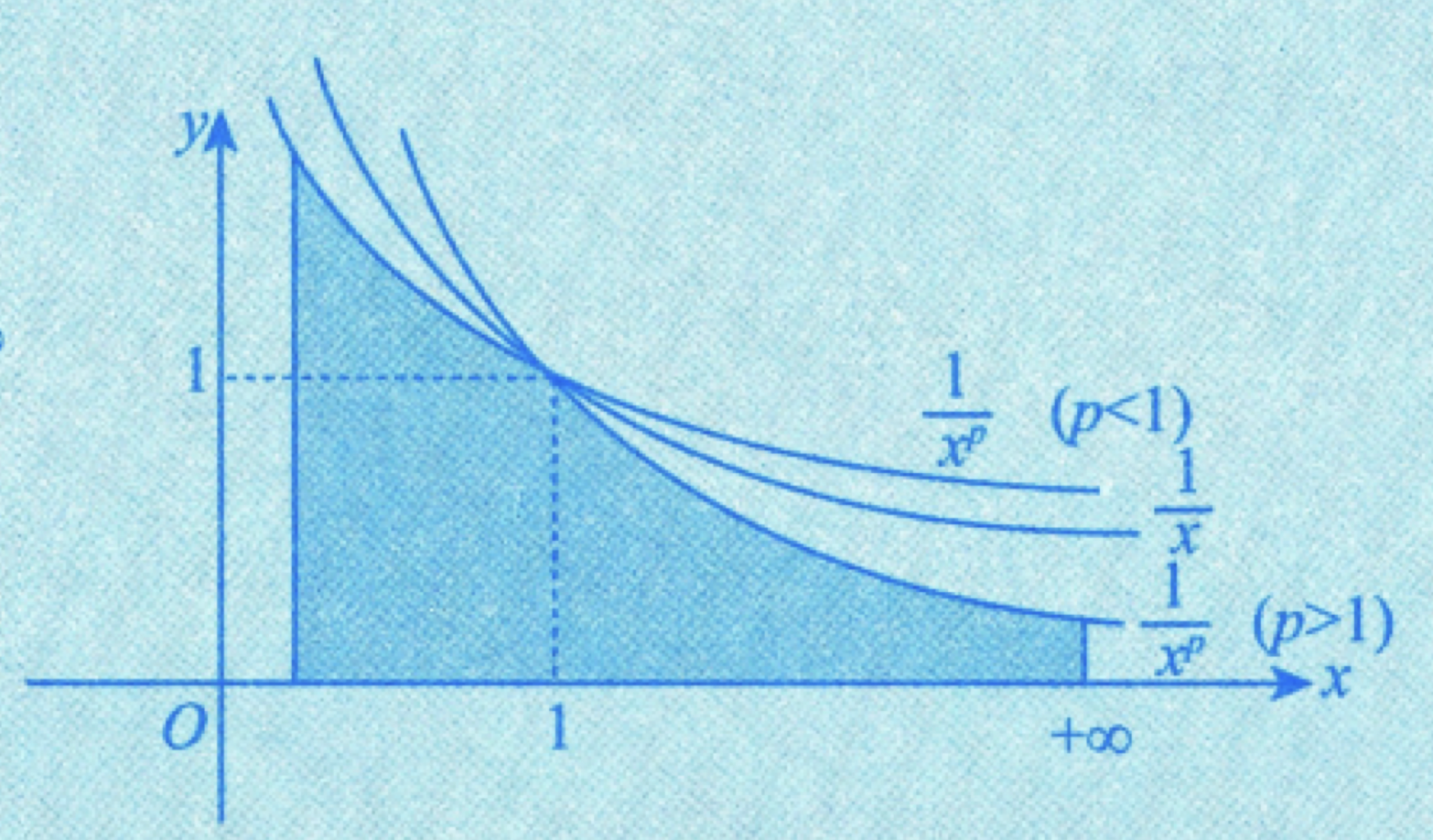
\(p\) 级数在 \(x=1\) 的时候发散,因为此时求积分得到 \(\ln x\),无论带入 \(0\) 还是 \(+\infty\) 都是发散的。